V matematice jako v dalších oborech narazíme občas na nějaké zkratky či symboly. Většina z nás prostě ví, že to něco znamená a když se opakují a my je potřebujeme, tak si je i zapamatujeme. Co ale tyto symboly R Q Z C N a další vlastně jsou? V dnešním článku vám přiblížím, co jednotlivé písmena znamenají a jak si je můžete zapamatovat, aby vám to už dávalo smysl?

Číselné obory
Matematika je obor, který se zabývá řešením problémů. Cílem je problém vyřešit a je jedno jak. Ve škole avšak se student nejčastěji potýkají obecně s čísly. Čísla rozdělujeme do několika skupin (kategorií), neboť každá skupina má podobné vlastnosti. Jednotlivým skupinám se říká obory čísel nebo číselné obory. Mezi ty základní obory patří:
- reálná čísla
- celá čísla
- přirozená čísla
- komplexní čísla
- imaginární čísla
- racionální čísla
- iracionální čísla.
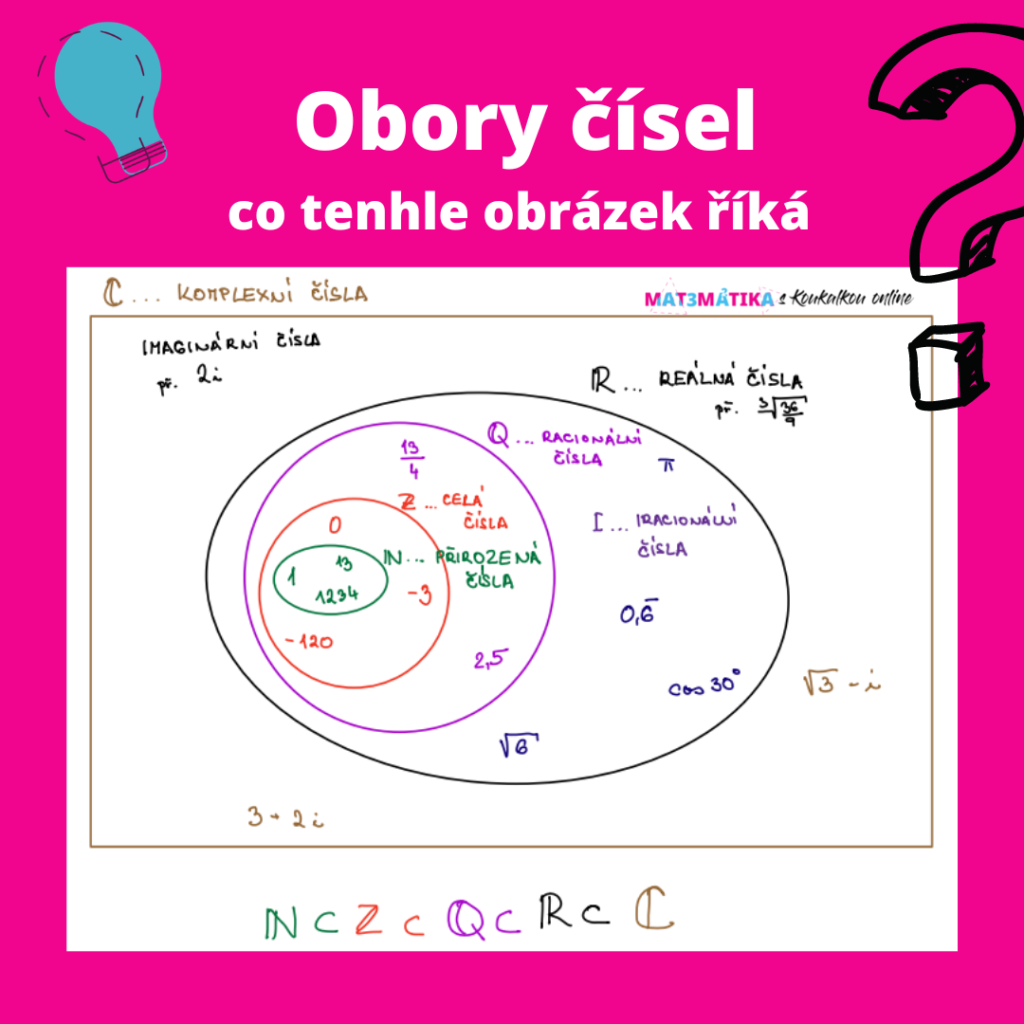
Možná jste si ve škole ukazovali obrázek výše, ale co vlastně říká? Je to vlastně jen grafické zobrazení množin (daných skupin číselných oborů) a podmnožin (podskupin). Většinou totiž jedna čísla můžeme zařadit do podskupin jiných ( v matematice říkáme, že množina jedněch čísel je podmnožinou druhých). Např. množina reálných čísel je podmnožinou čísel komplexních (tj. komplexní čísla jsou nadřazeny (obsahují v sobě) i reálná čísla). Pojďme si ale teď říci, co jednotlivé pojmy znamenají.
Reálná čísla
Reálná čísla (značíme R, nebo dvojitým R) … z latinského Real, anglicky Real numbers …. označuje skupinu všech čísel, která nejčastěji používáme (takže například zlomky, desetinná čísla, záporná čísla, odmocniny, intervaly, periodická čísla, nekonečně velká čísla). Tato skupina označuje pro studenty téměř cokoliv (takže i ta zvláštní čísla). Až na vybraných středních školách se potom student dozví, že existují ještě jedna skupina čísel, která je jim nadřazená – a to jsou čísla komplexní (o nich až níže).
\mathbb{R} => \frac{-13}{3}, log(12), e, \pi, 123.3325, \sqrt{265}, cos(30\degree), 124, -0.5, ...Racionální čísla
Do skupiny reálných čísel spadá i skupina racionálních čísel. Racionální čísla (značíme Q nebo dvojitým Q) … z latinského ratio (poměr) nebo Quotient (podíl), anglicky Rational numbers. Protože vychází z poměru/podílu, spadají sem zlomky, desetinná čísla (ty můžeme snadno přepsat do zlomku 😊 ). Do skupiny racionálních čísel spadají ale i další kategorie – celá čísla a čísla přirozená.
\mathbb{Q} => \frac{-13}{3}, -0.5 , 124, \sqrt{16} = 4, -1, ...Iracionální čísla
Opakem racionálních čísel jsou čísla iracionální. Iracionální čísla (většinou nenajdete žádné specifické označení, můžete narazit na I) jsou čísla, která nejsou racionální (z těchto pouček ve škole či na internetu jsem vždycky šílela, protože nic konkrétního nám to totiž neřekne). Možná pomůže poučka, že tyto čísla jsou taková, která nejdou vyjádřit zlomkem. Proto sem typicky spadají periodická čísla, odmocniny, logaritmy, konstanty – např. pí, eulerovo číslo.
\mathbb{I} => log(12), e, \pi, 123.333, \sqrt{124}, ...Celá čísla
Podskupinou racionálních čísel jsou čísla celá. Celá čísla (značíme Z nebo dvojitým Z) … z německého Zahlen – čísla. Tato skupina označuje jakákoliv záporná nebo kladná celá čísla (takže nesmí v nich být žádná část vyjádřena zlomkem či desetinným čísel) – prostě jen celky.
\mathbb{Z} => -5, -4, - \frac{12}{6} = -2, 13, 156, ...Můžete v některých publikacích narazit i na skupinu celých čísel takových, že jsou celá kladná včetně nuly. Označení najdete jako W (resp. dvojité W) z anglického Whole … celé, anglicky Whole numbers. Já jsem se s tímto pojmenováním ještě nesetkala a to ani u studentů, mezinárodních publikacích a na vysokých školách. Avšak to neznamená, že na něj nenarazíte vy.
\mathbb{W} => -5, -4, - \frac{12}{6} = -2, 0, 1, 13, 156, ...V českých školách se většinou potkáte s tím, že celá čísla značíme jako Z.
Přirozená čísla
Podskupinou celých čísel jsou čísla přirozená. Přirozená čísla (značíme N, resp. dvojitým N) z anglického Natural numbers, je skupina celých kladných čísel bez nuly. Tj. všechno, co je kladné a není to ve tvaru zlomku či desetinného čísla.
\mathbb{N} => 1, 2, 4, 150, ...Komplexní čísla
Všechny skupiny již dříve zmíněných číselných oborů spadají do skupiny čísel komplexních (komplexní čísla obsahuje všechny zmíněné). Komplexní čísla (značeno C, resp. dvojitým C) z anglického Complex numbers označují skupinu čísel, která obsahuje nejen všechna reálná čísla, ale i části imaginární. Každé komplexní číslo je totiž složeno z části reálné (Re) a složky imaginární (Im). Imaginární složka (část) je taková ta část, která obsahuje imaginární jednotku značenou i. Např. 3 + 6i.
\mathbb{C} => 3 + 6i, \sqrt{3i}, \frac{-13}{3}, log(12), e, \pi, 123.3325, \sqrt{265}, cos(30\degree), 124, -0.5, ...Asi si říkáte, a proč tohle všechno? K čemu slouží skupina komplexních čísel? Ono totiž popsat chování lidí, pohyb aut, migrace ptáků a vlastně všeho lze popsat matematickou rovnicí. A ne vždycky čísla vycházejí hezky (jako ve škole). Skupina komplexních čísel se nejčastěji využívá při různých zjednodušení, zápisů a výpočtů (např. u Fourierovy řady, zpracování signálu (např. zvuk, obraz, kvantové fyzice a dalších). Na vysoké škole můžete narazit na využití zejména u sinusů a kosinusů (zvuk je vlastně vlnění, které můžete rozložit na sinusoidy). Takže i když se vám zdá, že je toto členění absolutně zbytečné, věřte mi, že není. A pakliže budete studovat elektrotechniku či aplikovanou matematiku, narazíte na další a další využití v praxi.
Co znamenají symboly + – 0 u těch písmen?
Pokud chceme nějakou skupinu (číselný obor) vyspecifikovat, stačí specifikaci (čísla kladná, záporná, nula) vyjádřit pomocí symbolů +, -, 0. Takže například pokud hledáme celá čísla kladná a s nulou, symbol + a 0 k Z dopíšeme –> tudíž Zo+ (tímto způsobem můžeme vyspecifikovat jakékoliv obory čísel).
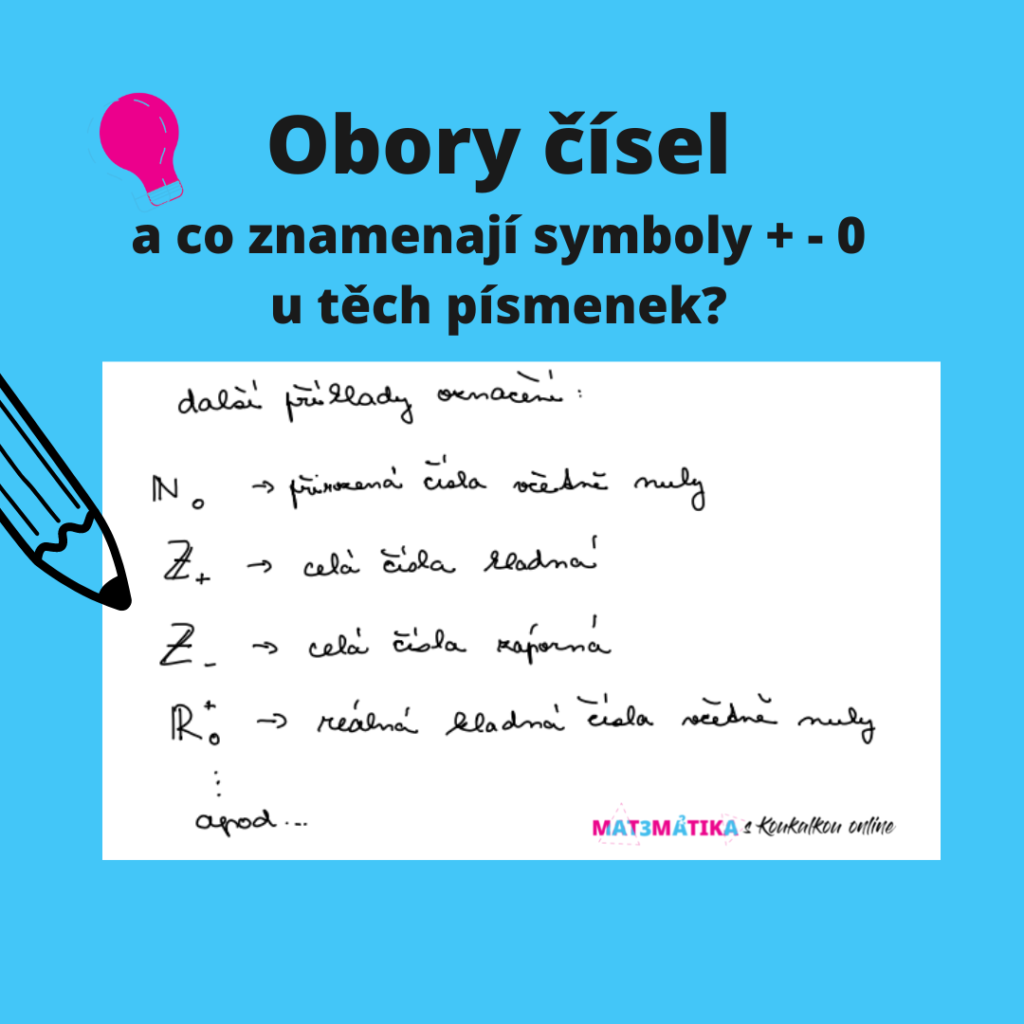
Kde se tyto zkratky N Z R nejčastěji používají?
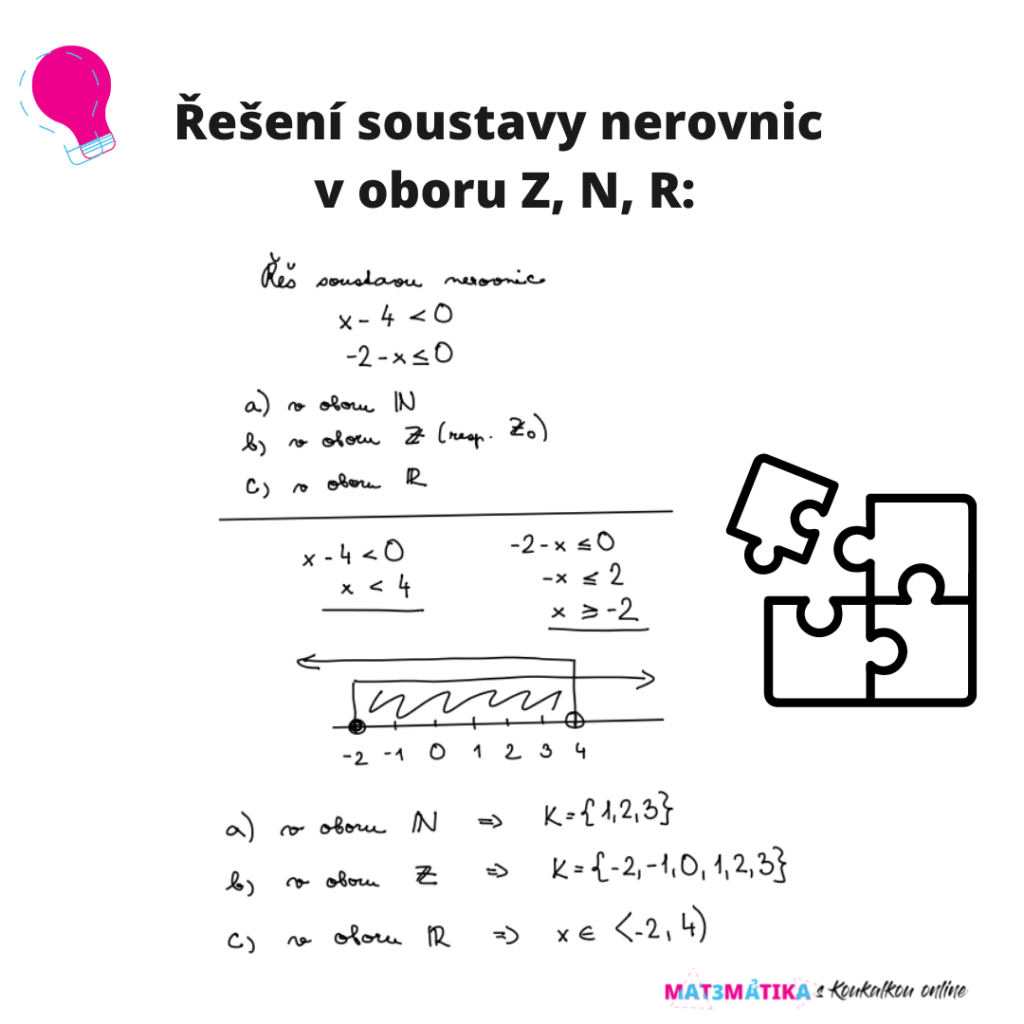
Všechny obory čísel (reálná, celá, iracionální, …) tedy mají své opodstatnění. Místo specifikace každého z nich využíváme mezinárodně platné symboly (písmena), které vycházejí většinou z anglického, německého či latinského pojmenování. Věřte mi, že toto označení vám ušetří do budoucna spoustu práce a vždy, když řešíte úlohu/příklad (např. ve škole), tak si přečtěte správně zadání. Řešení jednoho příkladu může být zadáno v různých číselných obor a tím pádem jsou různé výsledky. Mrkni na obrázek níže pro ilustraci.
Procvičuj
Tak a jak jinak něco dostat do hlavy než pomocí procvičování. Mám pro vás jedinečnou možnost a to zkusit následující kvíz. Tak co, jste připraveni?
A co dál?
Pomohl vám tento článek utřídit si myšlenky a zjistit, co ty písmenka R, N, Z, Q, C, W v matematice znamenají ? A nebo jste si vytvořili nějakou mnemotechnickou pomůcku pro to, aby jste si ty písmenka zapamatovali? Dejte mi vědět do komentáře, budu se na vaše příspěvky moc těšit.
Líbí se vám tento článek a chtěli by jste vědět víc? Ve VIP členské sekci totiž pro své studenty toho připravuji mnohem víc 😉 Je tam třeba matematická únikovka a spoustu videí k procvičení z různých zdrojů. Zajímá tě to? Mrkni se SEM.
A taky se můžete těšit na další článek. V některém dalším si totiž řekneme, jaké symboly v matematice nejčastěji využíváme a co znamenají, aby jste už nikdy nebyli zaskočeni.

